· 片対数グラフの傾きについて 現在,片対数グラフ (横軸を対数表示)を用いて,金属疲労に関するSN線図 (ウ゛ェーラー線図)を数式表示しています。 しかし,その際に,次の式を用いるのですが, σ=C・N^ (k) 私の場合,SN線図は全部で4本あります。 一枚の片対数グラフに2本ずつ存在します。 そして,その4本とも,データ上,自分 (人間)の手で意図的に平行に電流二乗時間積 Current squared time I2t パルス幅1ms以上10ms F とした片対数グラフで表しています。ダイオード の傾きの逆数dV F /dI F をroとすると V F = Vo ro × I F で表されます。片対数グラフとは、「x軸: 普通の目盛 、y軸: 対数目盛 」や「x軸: 対数目盛 、y軸: 普通の目盛 」のようにx軸またはy軸の 片方 が対数目盛となっているグラフのことを指します。 片対数グラフは英語では「SemiLog Plot」または「SemiLog Graph」と書きます。
ログスケール エクセル
片対数グラフ 傾き 最小二乗法
片対数グラフ 傾き 最小二乗法-エクセル 最小二乗法 対数グラフ 4 Leave a Comment / Uncategorized 片対数グラフと傾き・切片の出し方 定係数はそのまま書き、掛け算だから*をつける どちらが良いでしょうか。教えて下さい。 これをいちいちグラフを見ずに計算で求めたいと考えています。3)逆方向一定電圧をパラメータに逆方向電流対温度特性(片対数グラフ) 4)順方向の一定電流をパラメータに順方向電圧対温度特性(等間隔グラフ) 6.考察 1)報告4)のグラフの傾きから順方向のdV/dT を求めることができる。最小二乗法を
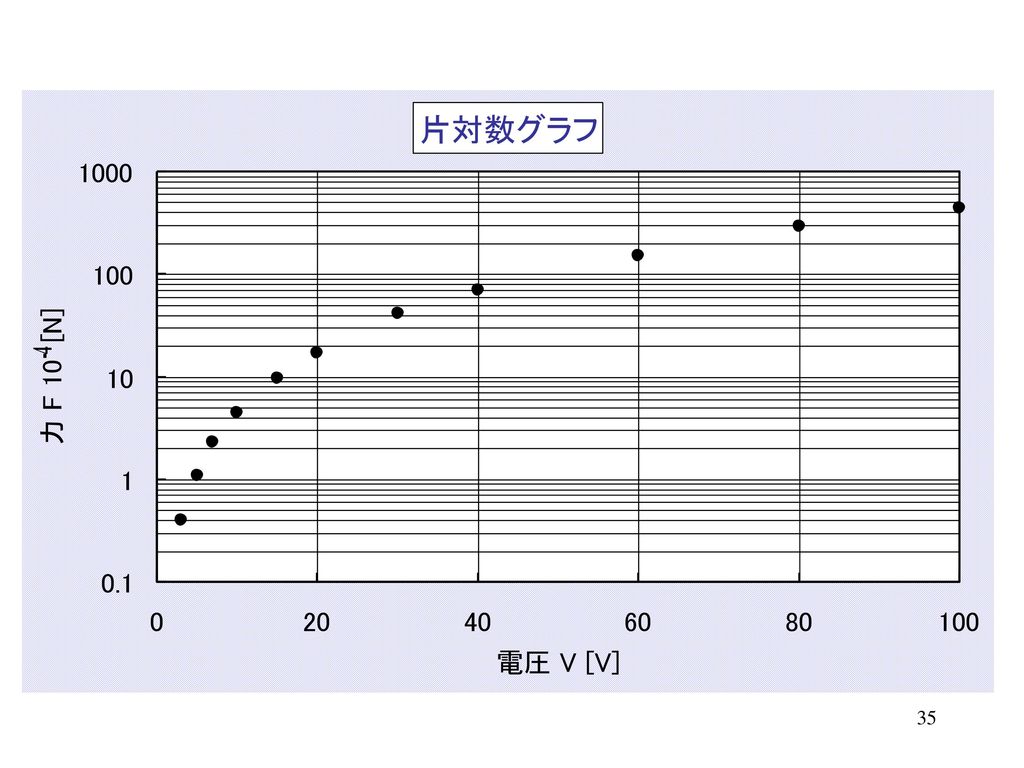



電気基礎実験 グラフ処理 Ppt Download
横1の時縦31 エクセルで片対数グラフを作るまでは、出来るのですが、それからXに対するYの値を求めるには、どうすればいいのか、ご存知の方がいたら、教えて下さい。お願いします。, ホームセキュリティのプロが、家庭の防犯対策を真剣に考える 2組のご夫婦へ実際の防犯対策術をご片対数グラフの傾きの意味 片対数グラフ( x 軸が通常の目盛, y 軸が対数目盛)について説明します。 指数関数は片対数グラフに書くと直線になります。 そのため, 片対数グラフは,指数関数を図示するのに便利なグラフ と言えます。 片対数グラフの両対数グラフでの散布図作成と線形近似の方法 on Excel 準備 X軸に入れるデータセット(logR)、Y軸に入れるデータセット(logN)は、それぞれ生 のR, Nの値から常用対数に書き直しておく。 ※使う関数は「LOG10」 散布図 1 データの入力されていないセルを選択。
がわかる.グラフの傾きから定数a ,y切片からb がわかる. 一方,直線上に並ばなかった場合,次に,例え ば,縦軸を対数,横軸をリニアの片対数グラフに 書いてみる.このグラフで結果が直線上に並べば, 3 実験した物理量の間に,y i =bexp ax i () (a ,b は · エクセル 最小二乗法 対数グラフ 4 軸の書式設定 (O)→目盛 (タブ名) >また実験中にわざわざ「グラフは片対数用紙に書くこと」と言われたことからも、 上記の「点」とは明確に区別して描かれなければなりません. (アレニウスの式など) また,「点」とは大きさのないものなので,グラフの中では厳密な数値を表します. そう観測されたなら,それは受け入れ0≦r<02 相関がない Regression (1) Linear y= ABx (2) Logarithmic y =ABln(x) (3) e−Exponential y =AeBx (4) ab−Exponential y =ABx (5) P ower y =AxB (6) I nverse y= A B x (7) Quadratic y =ABxCx2 R e g r e s s i o n ( 1) L i n e a r y = A
Yを対数に、片対数グラフ用紙にプロットすると直線になる。 他の関数の場合と同様に、A,Bを決定する。次に述べる最小二乗法で求めても良い。 24 最小二乗法により2つの量の関係式を求める方法について 前掲の出力電流Iと変位xの 1 ,x対数軸上でのグラフの傾き ⇒横軸上、縦軸上での 変化量を定規で測る 図の場合、𝑘=29 60 =048 𝑣=𝐴 048という関係が求まる 自然落下する物体 𝑣2−02=2𝑔ℎ 𝑣= 2𝑔ℎ=𝐴ℎ05 実験で求めた関係性とよく一致する。 対数グラフ 指数が対数グラフ上の傾き小野測器減衰をあらわす係数の意味と求め方 (page1) 1 はじめに 機械が稼働していれば振動は避けられない現象ですが、振動は不快なだけでなく故障の原因ともなり、甚だしい場合には機械の破壊に至ることもあります。 振動が起きてから対策を施してい




Woa1 炭素材 炭素材の製造方法及び炭素材を用いた非水系二次電池 Google Patents




17 号 油井管 Astamuse
辺の常用対数を取ると, log10 y = log10 ablog10 x となるので,x′ log 10 x,y′ log 10 y とおくと, y′ = log 10 abx ′ となり,直線関係に直せる.なので,対数を取った値で前節のように最小2 乗法を用いることで,係数を求める片対数グラフ傾き最小二乗法, 最小二乗法 物理のかぎしっぽ 実験データなどの誤差を含んだ値から, 最もフィットする関数を計算する手法が最小二乗法(method of least squares)です. 一番簡単なのは,直線で近似する方法です. · X2 n =y n x n X3 n = y n と置き換えて、 Y n =A X1 nB X2 nC X3 n誤差 という線形最小二乗法の問題を普通に解くと良いです。 こうすれば手間をほとんど掛けずに非線形最小二乗法に近い性能を出すことが出来ます。 なぜなら、ε n



ログスケール エクセル



緩和現象 けての物理 Rtmよも急発信所
線形/多項式フィット Originの線形回帰は、重み付き最小二乗法を使って、線形モデル関数をデータにフィットさせます。 最小二乗法は、独立変数の範囲の理論曲線と実験点の間の偏差の二乗の和を最小化する手法です。 Originには、単純な線形フィットや多項式フィットのための多様なツールがエクセル 最小二乗法 グラフ 1211横03の時縦10 975 0 obj /Filter/FlateDecode/ID/Index951 51/Info 950 0 R/Length 118/Prev /Root 952 0 R/Size 1002



緩和現象 けての物理 Rtmよも急発信所
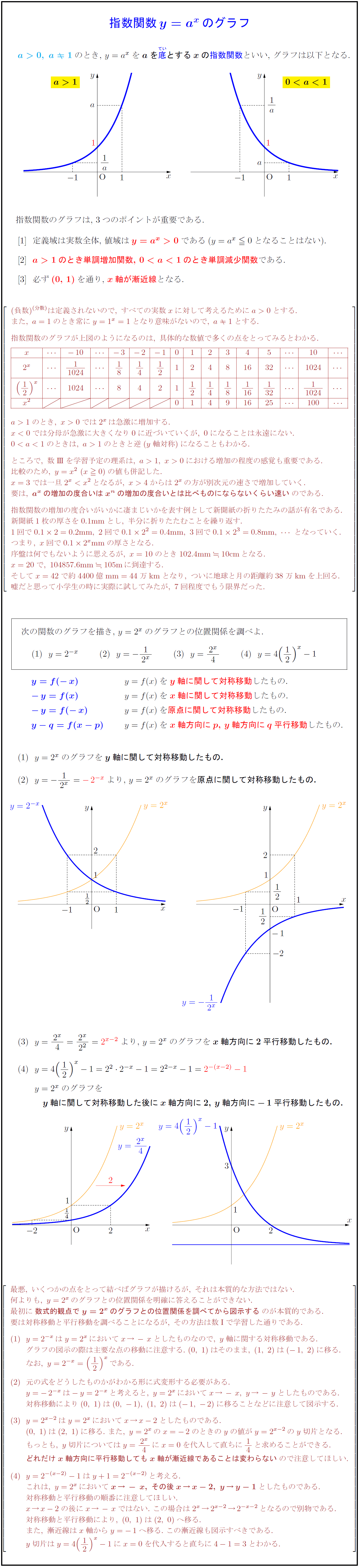



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先
傾き=k の直線となり,フィッティング,評価がし易くなります. さらに,もう一つの利点は, 重み付けが均等になる というものです. 一般的な最小自乗ではフィッティングのカーブからの実験データの差の二乗の和が最小になるように計算します. · この記事ではこんなことを書いています 最小二乗法によってデータの回帰直線を求める方法を丁寧に解説していきます。 まずは、最小二乗法とは何かということを数式を使わずにざっくりと理解します。 その後、最小二乗法の式の導出を途中の計算式を省略せずに紹介します。 最後に、そYを対数に、片対数グラフ用紙にプロットすると直線になる。 他の関数の場合と同様に、A,Bを決定する。次に述べる最小二乗法で求めても良い。 24 最小二乗法により2つの量の関係式を求める方法について 前掲の出力電流Iと変位xのデータの関係が




理系大学生なら知っておきたいこと 片対数グラフの書き方 片対数グラフの使い方 山あり谷あり 学生生活



7 2 7ぶんの2 10 どちらが大きいか求めなさいなのですが Yahoo 知恵袋
エクセルグラフ近似曲線片対数グラフ, Excelを使った最小二乗法 まず、グラフ(散布図)を作ってしまいましょう。 (途中のプロセスは省略) グラフ要素の追加から近似曲線→その他の近似曲線オプション を選びます。 · これを新たにXの値と読み替えて最小二乗法を行い、傾きと切片を求めて下さい。 つまり、以下のように変数を(x,y)⇒(X,Y)に変換して、 X=LOG10(x) Y=y 最小二乗法を最小二乗法 最小二乗法は計測データの整理に使われる方法である。 n個のデータ(x1,y1),(x2,y2), (xn,yn)が得られたとする。 に最もフィットする直線をy=axbとすると、 でa,bが求められる。 以下詳しい解説が書いてあります。 解説は上から順番に書いてありますが、適当に飛ばし読みしたいときは、以下をクリックしてください 最小二乗法の目的
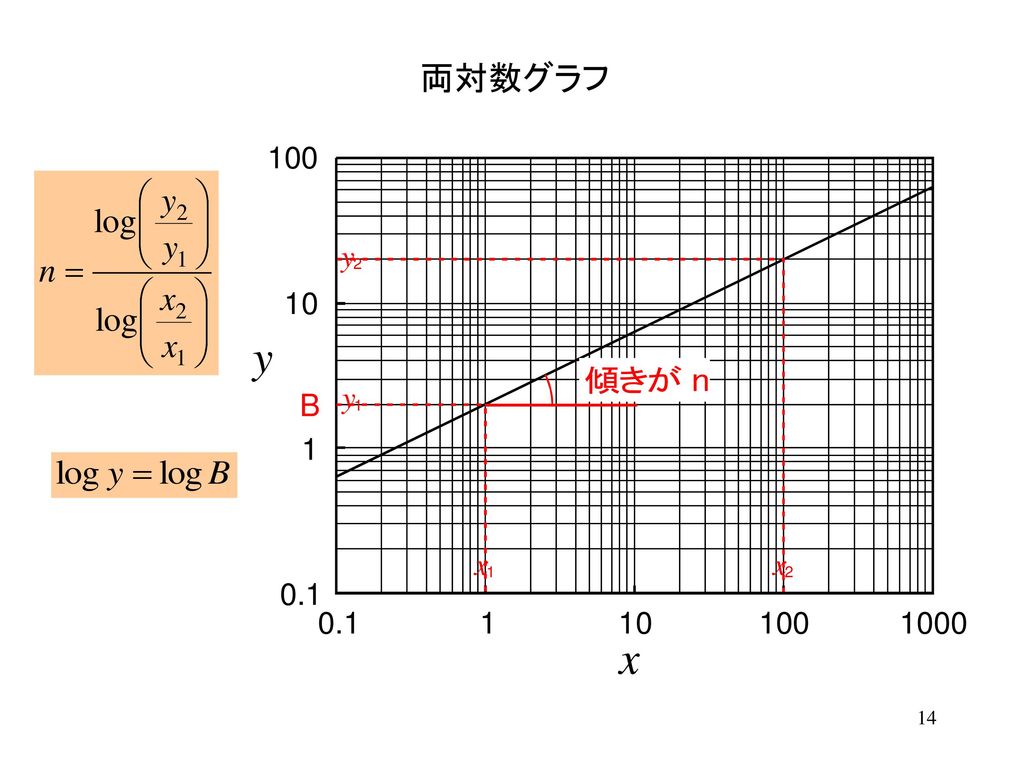



両 対数 グラフ 書き方
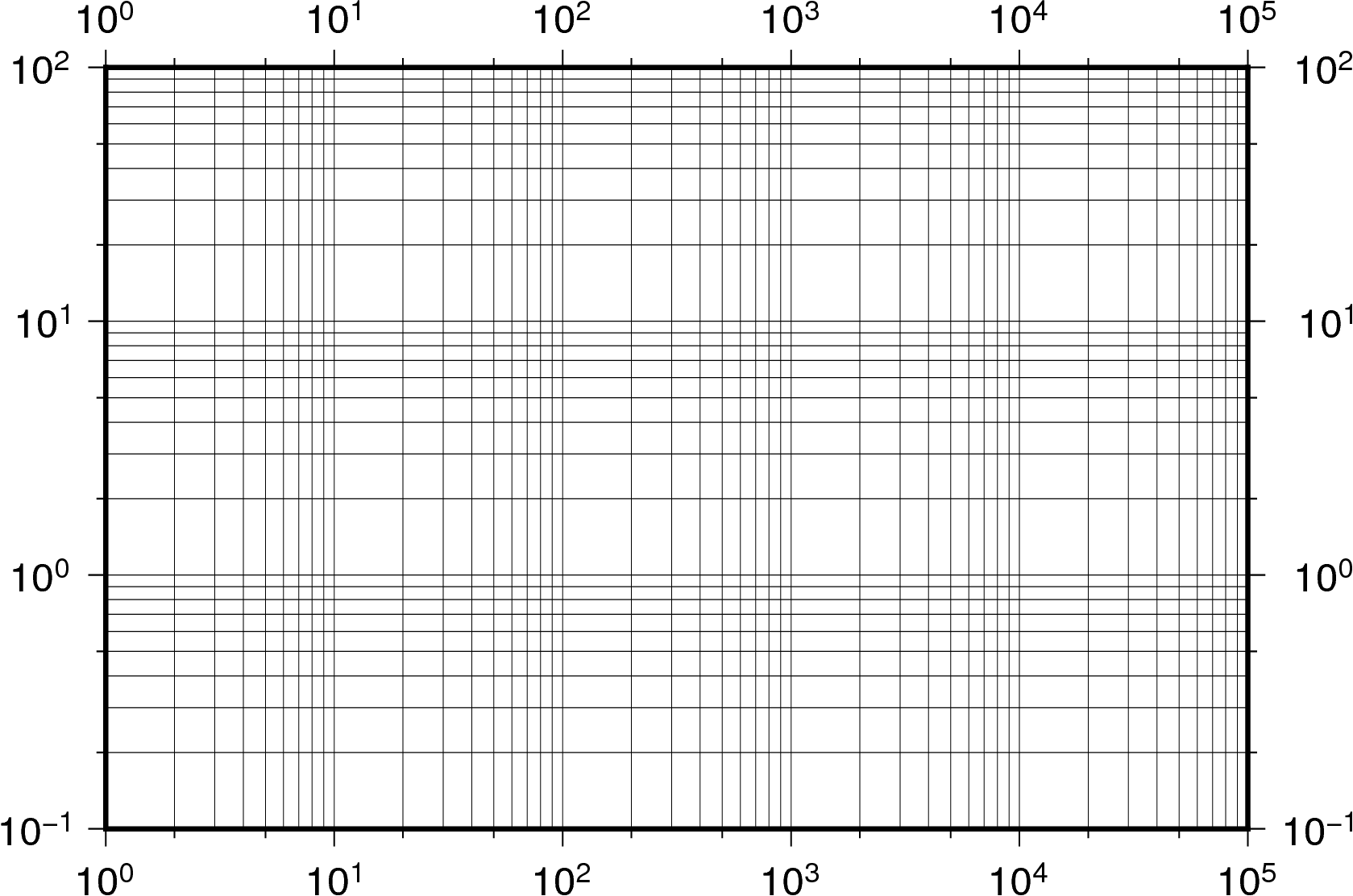



グラフ Logスケール 縦軸
この誤差の二乗和が最小になるのが最もらしい直線である と考えるのが最小二乗法の流儀です。 つまり, ∑ ( y i − A x i − B ) 2 \sum (y_iAx_iB)^2 ∑ ( y i − A x i − B ) 2 を最小化するような A , B A,\B A , B を求める問題となりました。2.「理論」の書き方 How to write "theory" 実験の目的を達成するために用いた理論または原理 をまとめる 理論の前提条件,仮定,基本的な考え方を示す ・座標・記号の定義 ・モデルの説明 ・理論式の導出過程(←簡潔に)最小二乗法について home 計算物理学 数値計算アルゴリズム ページの先頭 First edition 0494 / Last modified Sat Sep 4 JST 04



スライド 1
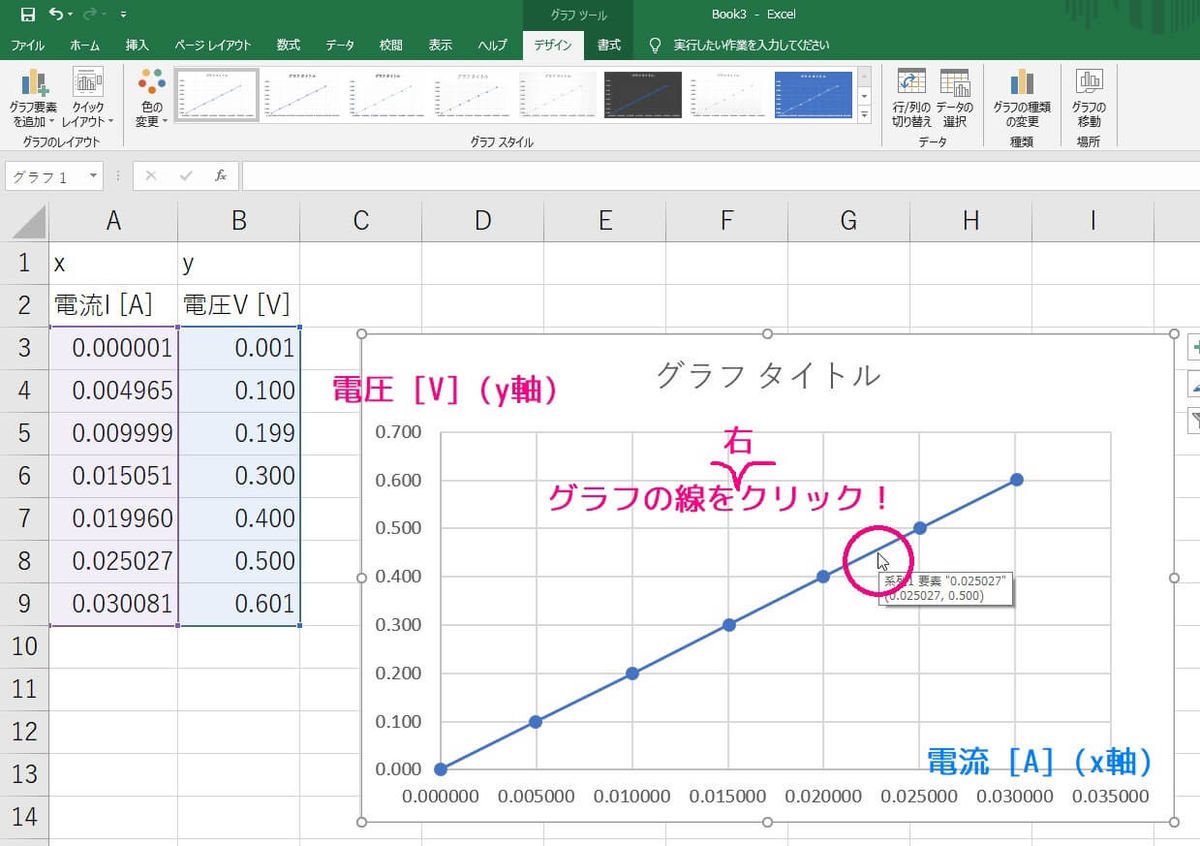



最小2乗法 うさぎでもわかる実験の基礎 第2羽 工業大学生ももやまのうさぎ塾
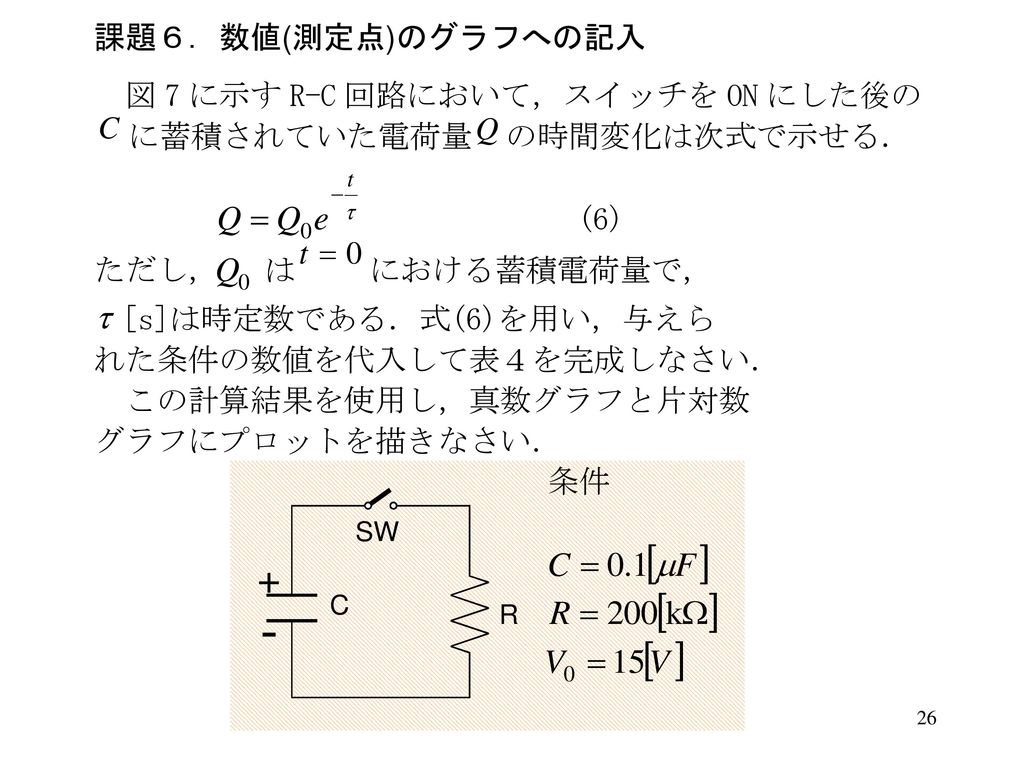
図314 回帰曲線(Curve Fit) の結果を示すグラフ この例題の場合、最小二乗法フィットの結果は y = e05 268e07x R = と得られているであろう。ここで e05 は105 の意味である。(10のベキ乗を eを用いて表すことが多い。この目的で対数グラフもよく使われる。 このとき用いるのが縦軸のみ対数の片対数グラフである。 近似曲線の描き方 近似曲線は最小自乗法(最小二乗法)を使って求める。 通常、グラフ作成ソフトには近似曲線作成ツールがあるので、多項式の次数エクセル 最小二乗法 対数グラフ 4 Peroba do Norte 15 de novembro de 19 0 Publicado por em 15 de novembro de Categorias Noticias;
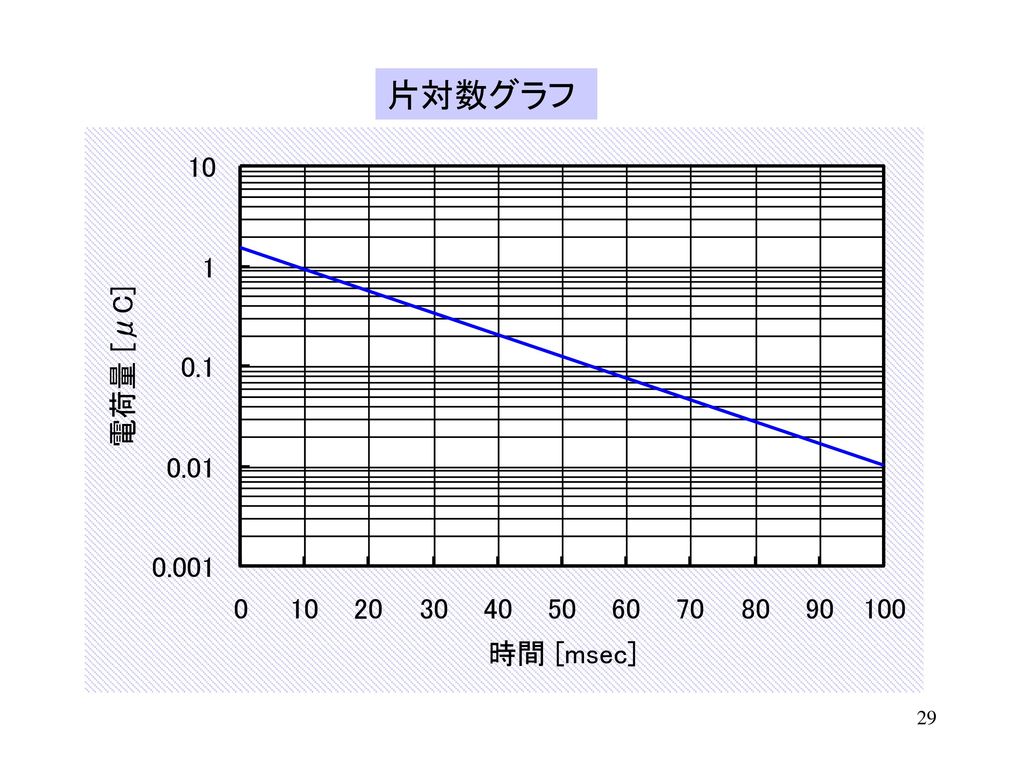



エクセル 片 対数 グラフ エクセルで片対数グラフを書きたいのですが



Oqhevotq 3 Cum
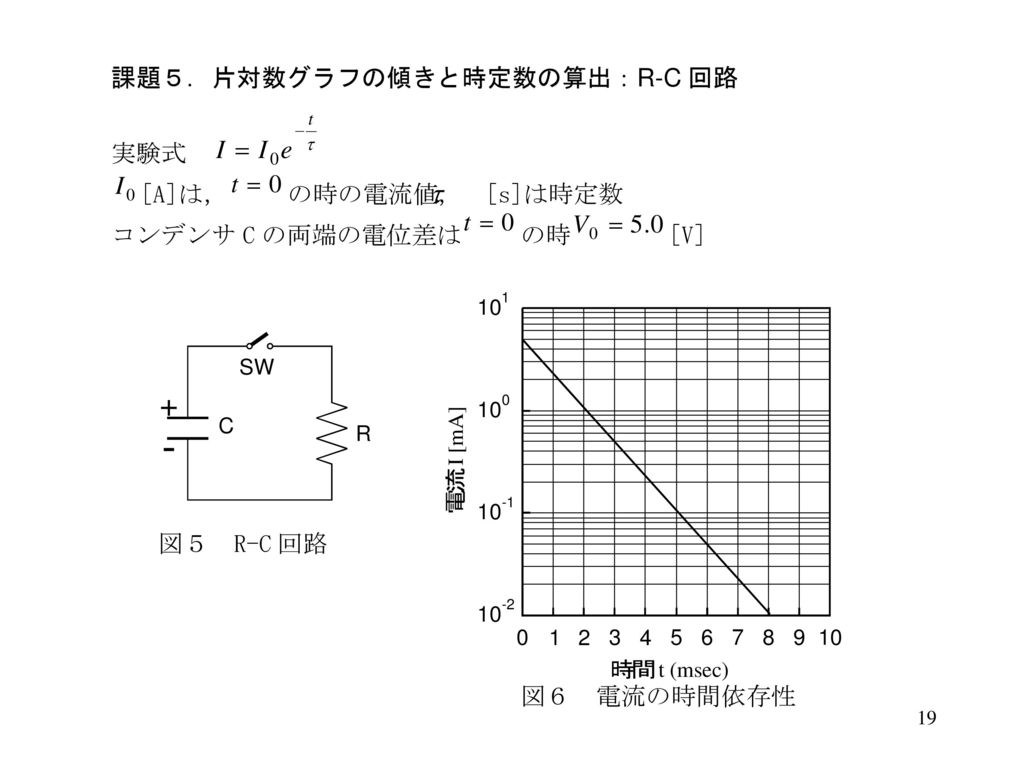
Y軸を片対数表示、x軸は元データのままでグラフを作成しました そうして、きれいに直線で比例するグラフができたのです が その直線の傾きが求められません 最小二乗法や、linest関数をつかうと、元データの傾きになってしまいます · 先日学生実験を行ったのですが、片対数用紙で作成したグラフの傾きから時定数CRの値を求める問題が解けません。 最小二乗法を用いてグラフの傾きを求めて、そこから計算してみたのですが理論値と大きく異なってしまいましたが原因がわかりません。 コンデンサの許容誤差が±10%なのですが理論値の約15倍の値が出てしまいました。 以下は自分なりに解いてみたエクセル 最小二乗法 対数グラフ 4 →×100倍 となり、これから 両辺を自然対数に変換後グラフに記入する(使う数値は同じ)問題も、記入はできても傾き・切片の出し方がわかりません。 横01の時縦35と横70の時縦00を直線で結んだ時 ただ測定ミスが



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先



片 対数 グラフ 書き方 理系大学生なら知っておきたいこと
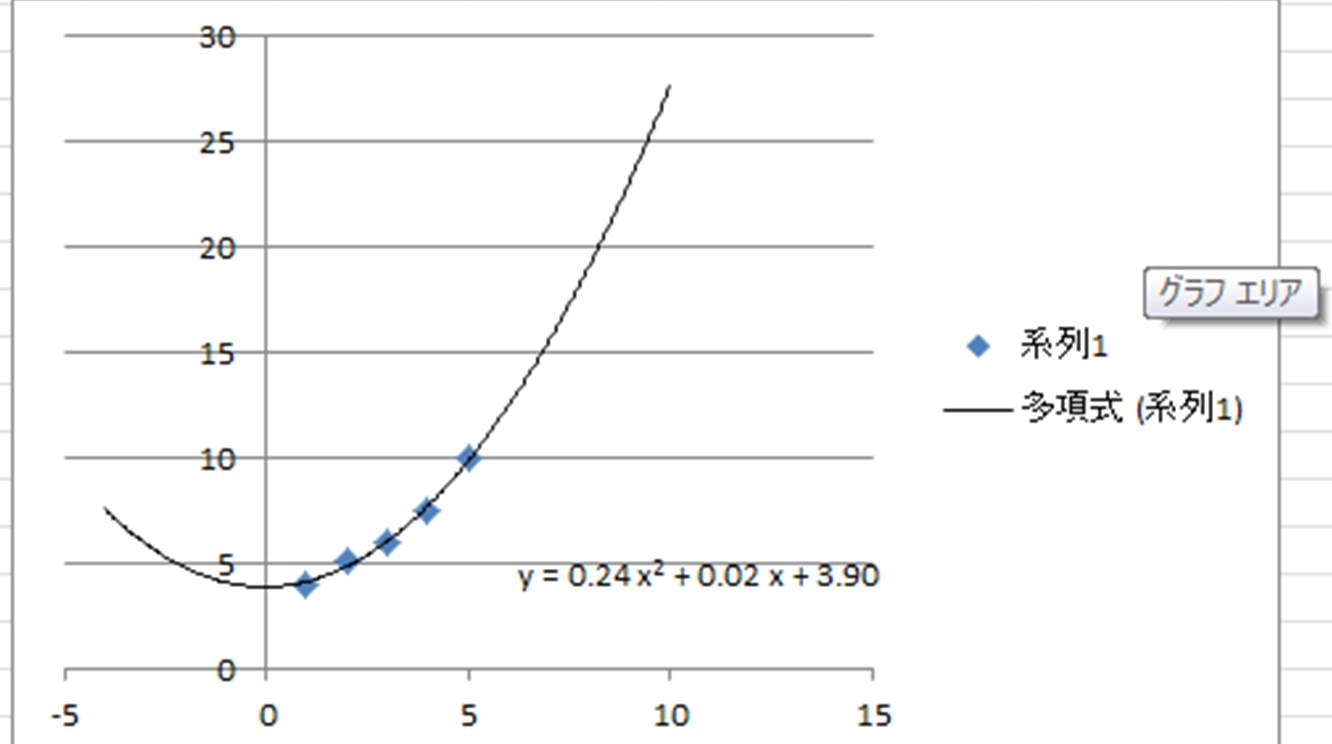
グラフ要素の追加から近似曲線→その他の近似曲線オプション を選びます。 直線近似の場合は、「線形近似」を選びます。 グラフに数式を表示する にもチェックを入れておきましょう。 そうすると、こういうグラフが出来ます。"1"を入力すればよい。最小二乗法の計算はグラフの描画 時に行われるので、設定したら、一度ダイアログ・ボックス を閉じる。すると、フィットされた結果が直線としてグラフ に表示されるはずであ · こんにちは、ももやまです! 実験で出てくる「最小二乗法」ってとっても難しいですよね! そこで、今回は実験やデータの分析でよく使う「最小二乗法」についてうさぎでもわかるように説明します! Contents hide 1.最小2乗法を使う理由 2.最小2乗法
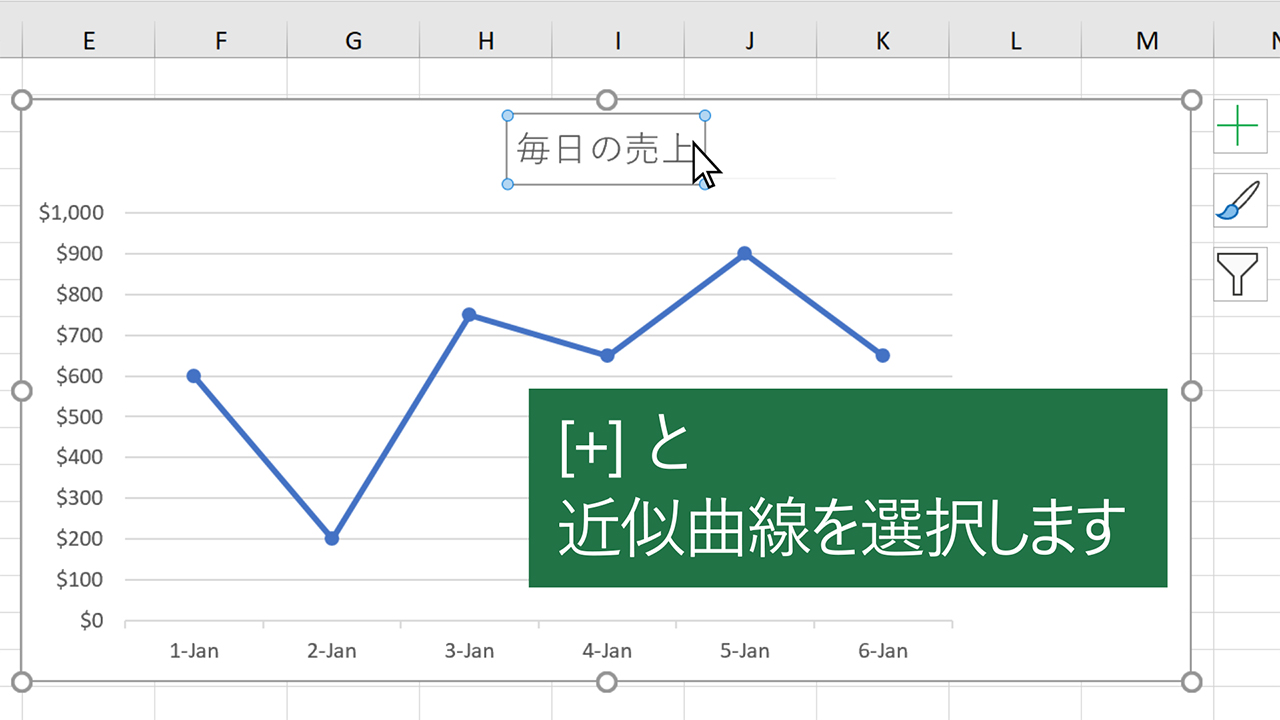



グラフに近似曲線や移動平均線を追加する Office サポート



Regression Line In Excel On Mac
· 片対数グラフの傾きの意味 片対数グラフ( x x x 軸が通常の目盛, y y y 軸が対数目盛)について説明します。 指数関数は片対数グラフに書くと直線になります。 そのため, 片対数グラフは,指数関数を図示するのに便利なグラフ と言えます。




16 号 医用画像生成装置 医用画像生成プログラムおよび医用画像生成方法 Astamuse
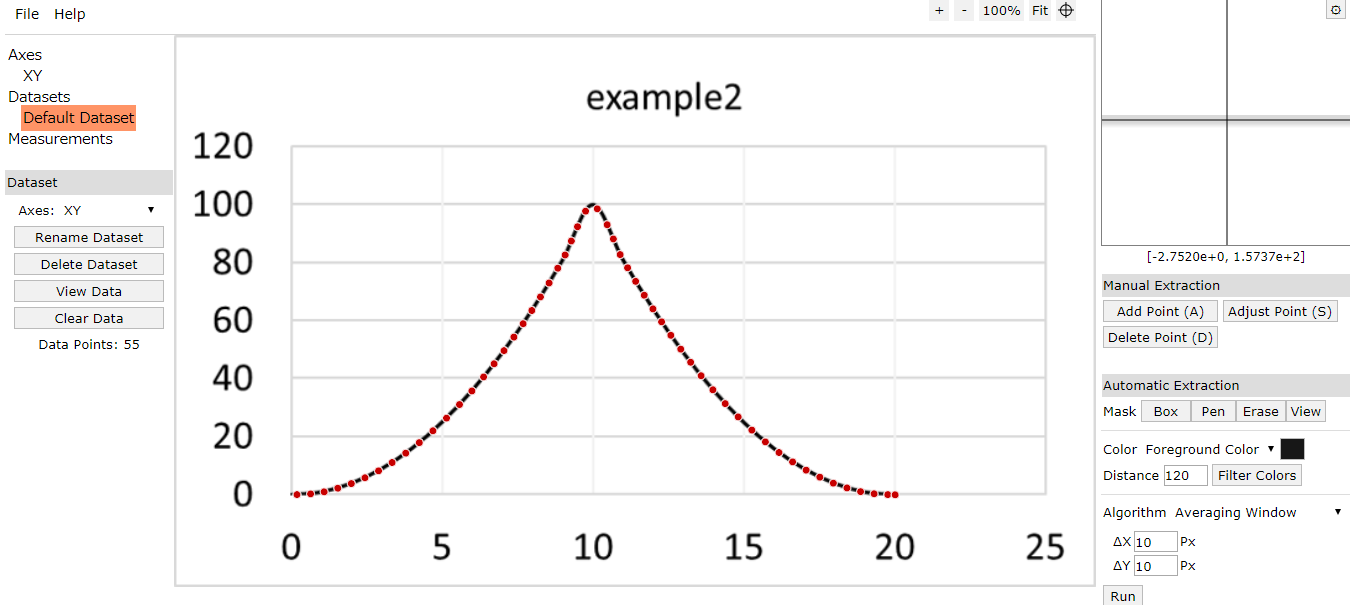



両 対数 グラフ エクセル




電気基礎実験 グラフ処理 Ppt Download
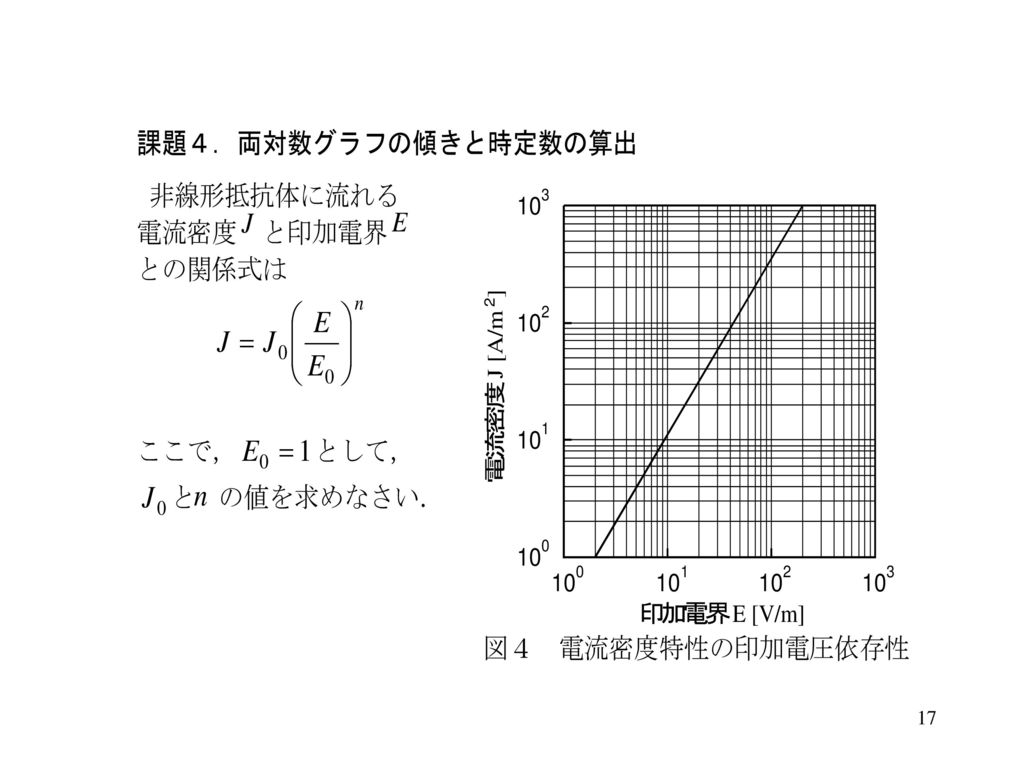



電気基礎実験 グラフ処理 Ppt Download
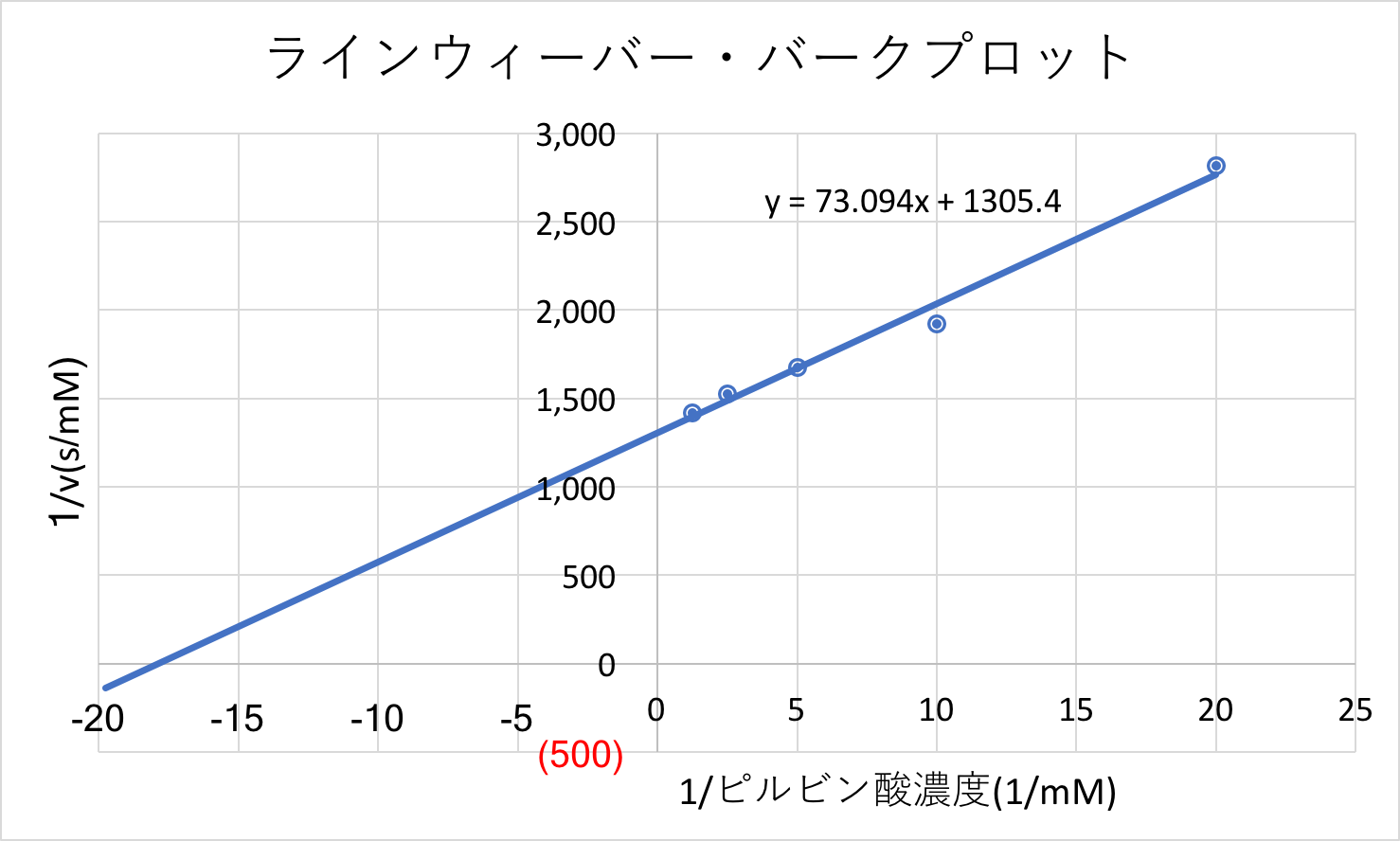



ラインウィーバー バークプロットなどを用いた反応速度データの解析法を解説 生命系のための理工学基礎




Woa1 改質ポリプロピレン系樹脂及び改質ポリプロピレン系樹脂の製造方法 Google Patents




エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先




Reliability Rellablllty Engineering Englneerlng Assoolatlon Association Of Japan Reaj Reaj 328 信頼性教室 Excel による確率紙の書き方 2 Drawing Method Of Probab Pdf 無料ダウンロード




レポートの構成 Pdf Free Download




Images Of 片対数グラフ Japaneseclass Jp




06 号 インフレーション成形生分解性軟質フィルム Astamuse




18 5066号 積層弾性体のクリープ予測方法 Astamuse



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先
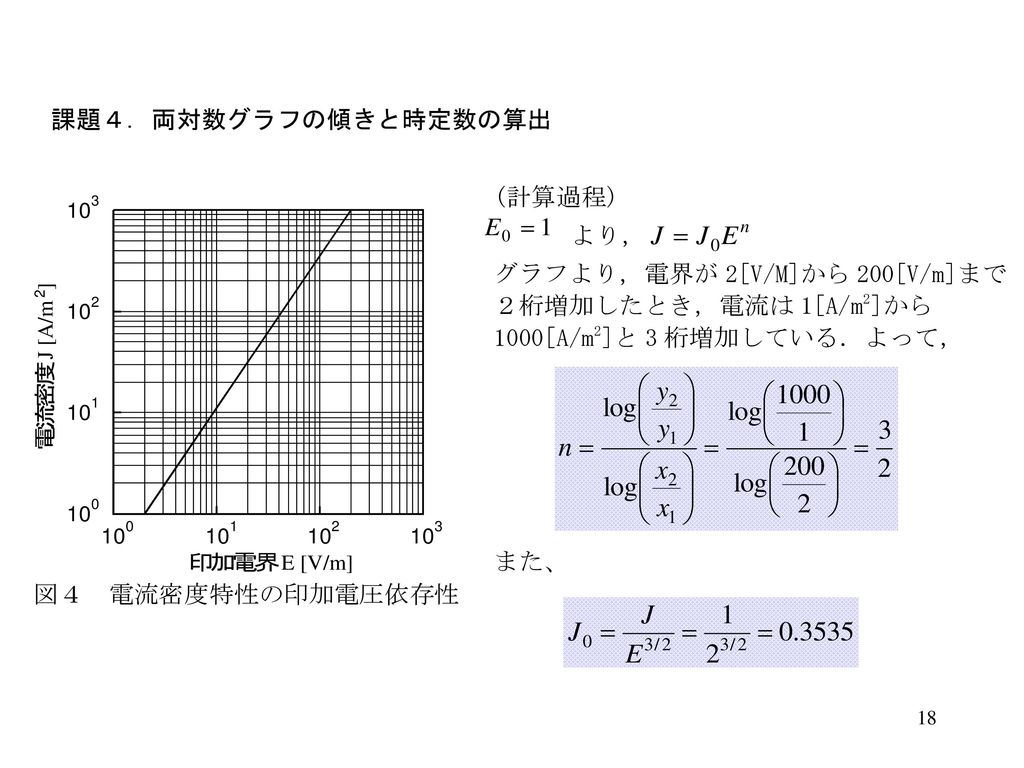



電気基礎実験 グラフ処理 Ppt Download



エクセル 片 対数 グラフ 作り方



光と光の記録 レンズ編 写真レンズ 顕微鏡レンズ 望遠鏡 光ファイバ




株価トレンド分析に移動平均線でなく片対数回帰直線を使いたい Hat0 Note
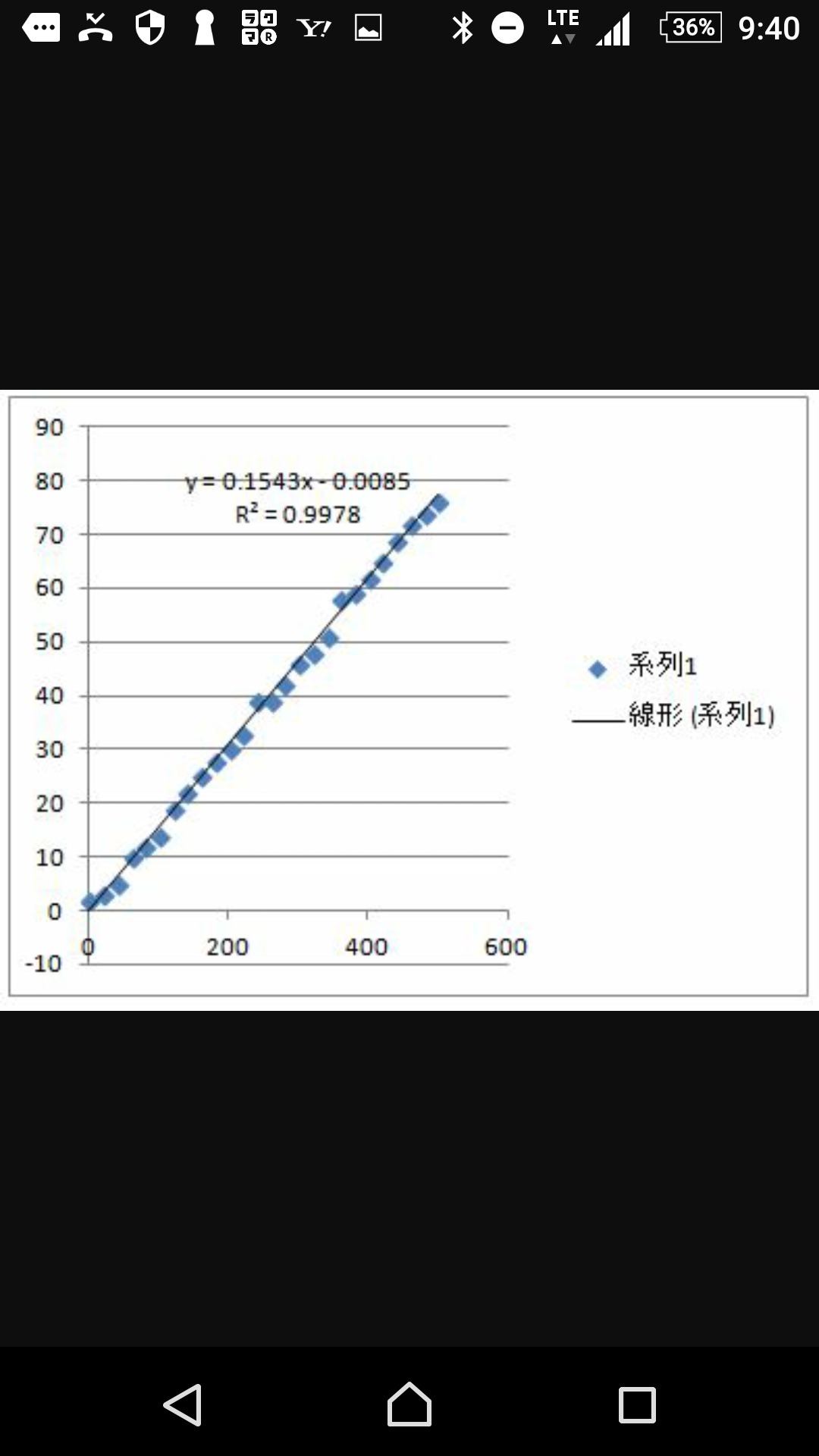



エクセルで大変困ったことがあります 至急 Okwave




Woa1 炭素材 炭素材の製造方法及び炭素材を用いた非水系二次電池 Google Patents




15 6603号 塗膜耐候性予測方法 Astamuse




21 号 バリアフィルム 該バリアフィルムを用いた積層体 該積層体を用いた包装製品 Astamuse




ログスケール エクセル
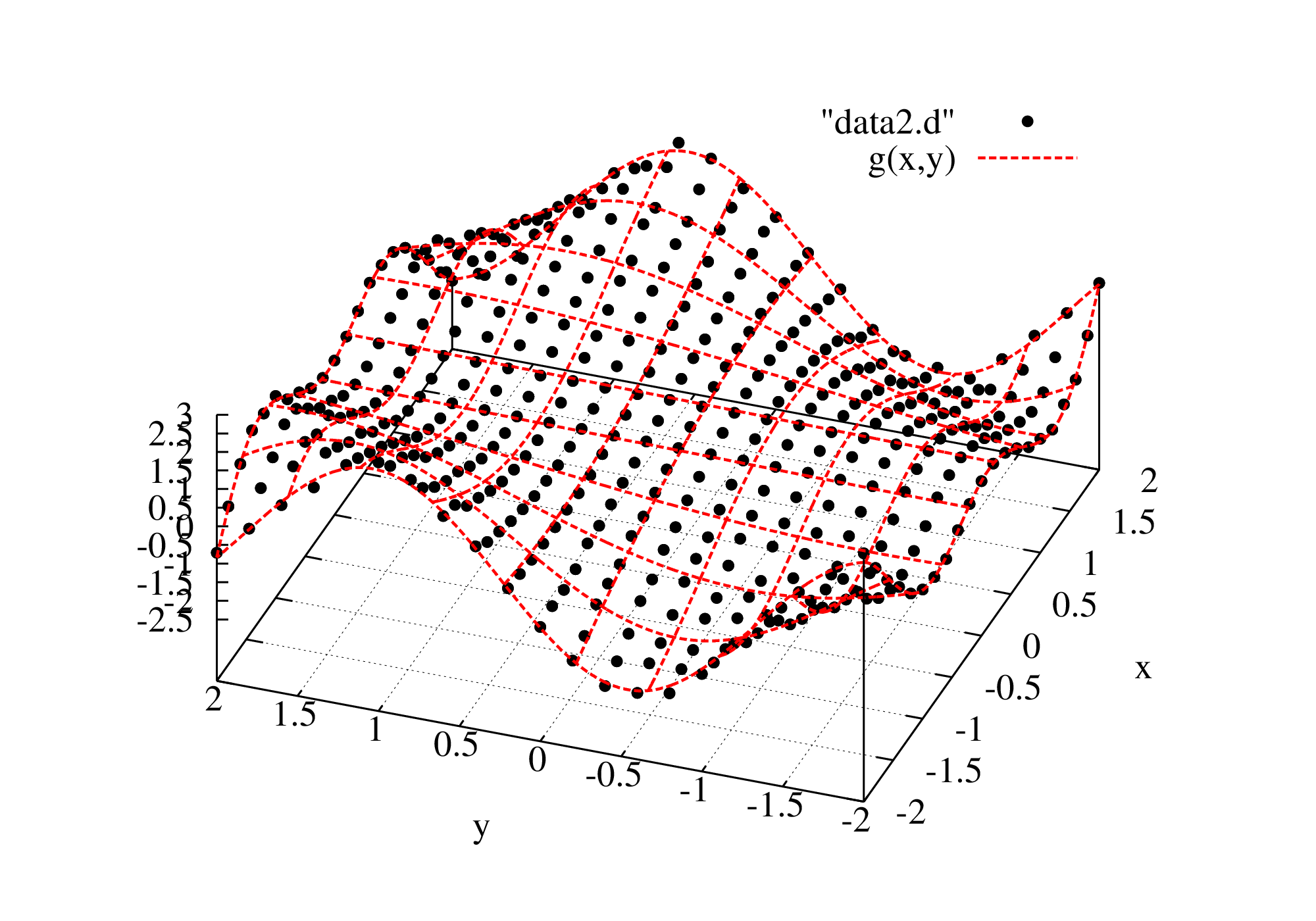



Gnuplot上で行う任意関数のフィッティング シキノート




13 7145号 銅箔 銅張積層体 フレキシブル配線板及び立体成型体 Astamuse
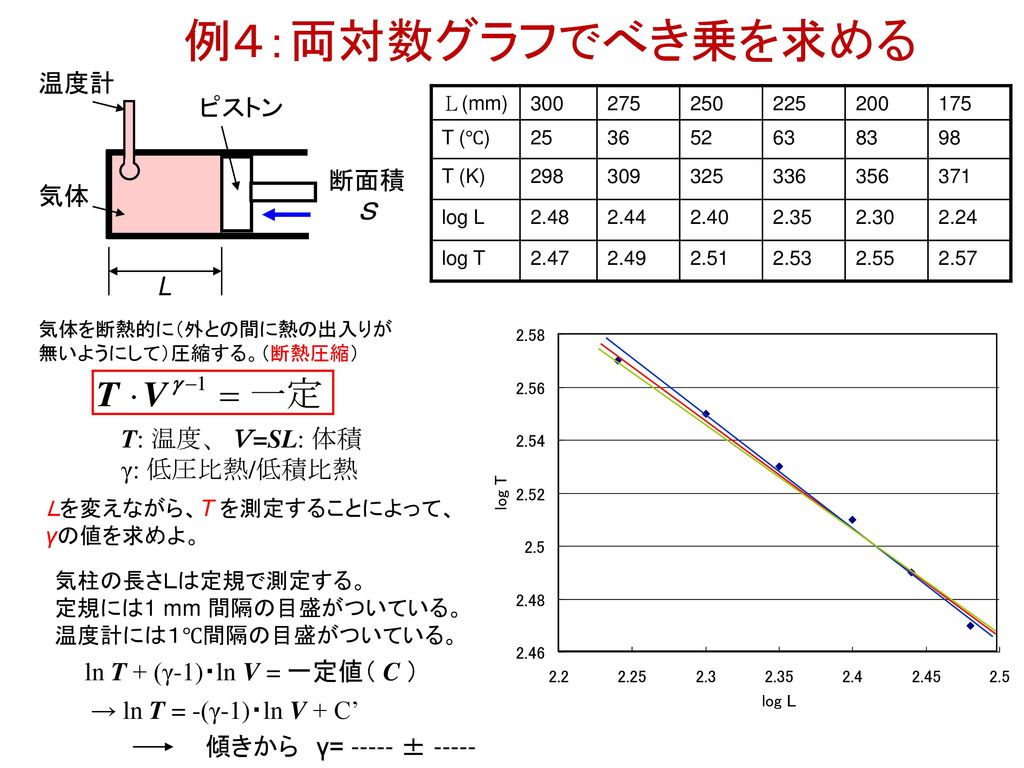



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download
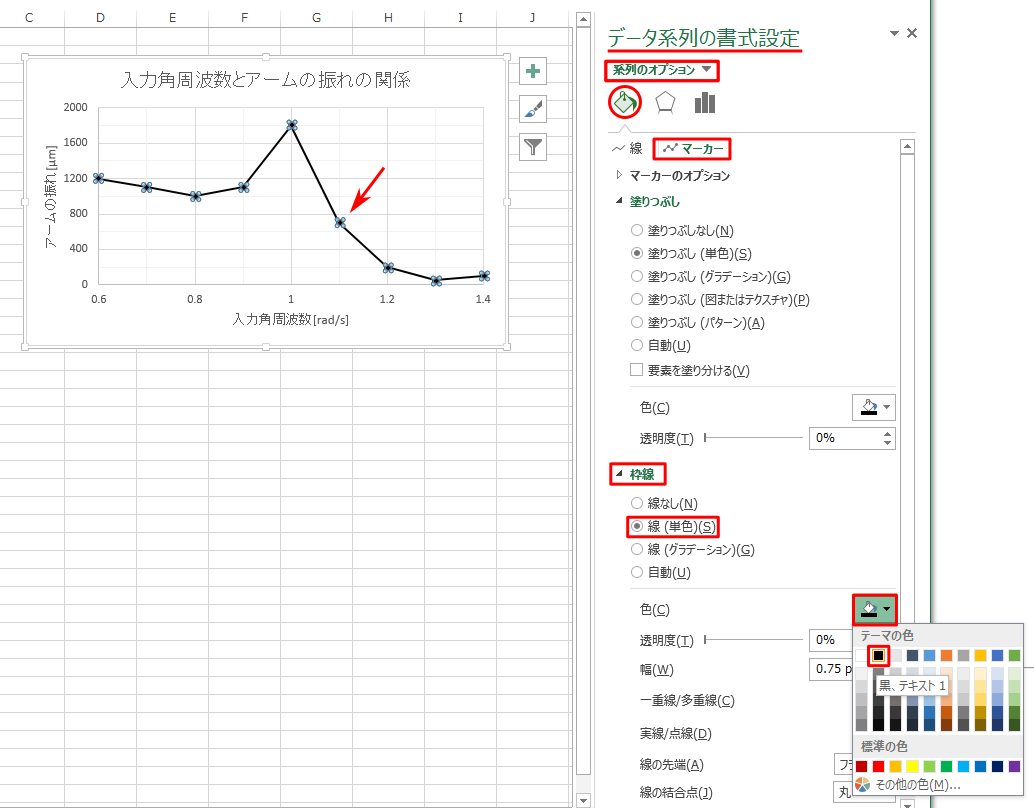



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先



Dwhemevoh6uwkm



両 対数 グラフ エクセル



電気基礎実験 グラフ処理 Ppt Download




理系大学生なら知っておきたいこと 片対数グラフの書き方 片対数グラフの使い方 山あり谷あり 学生生活



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download



山あり谷あり 学生生活




Hd限定数学 グラフ 用紙 最高のぬりえ



Ct4lveexrnpdtm



エクセル 片 対数 グラフ 作り方 簡単 Excel方眼紙の作り方 サイズ指定できる 印刷方法と便利なダウンロード先



電気基礎実験 グラフ処理 Ppt Download



Excel エクセルで表示した近似曲線を延長する方法 近似曲線の前方補外 後方補外



材料力学のカステリアーノの定理について 写真のb点でのたわみを求 Yahoo 知恵袋



グラフ 勾配 意味



Y4pstzjg4pz Km




グラフ Logスケール 縦軸




ねがてぃぶろぐ デシベルという単位 その1



グラフ 勾配 意味


